1.1.6. Boolean Functions
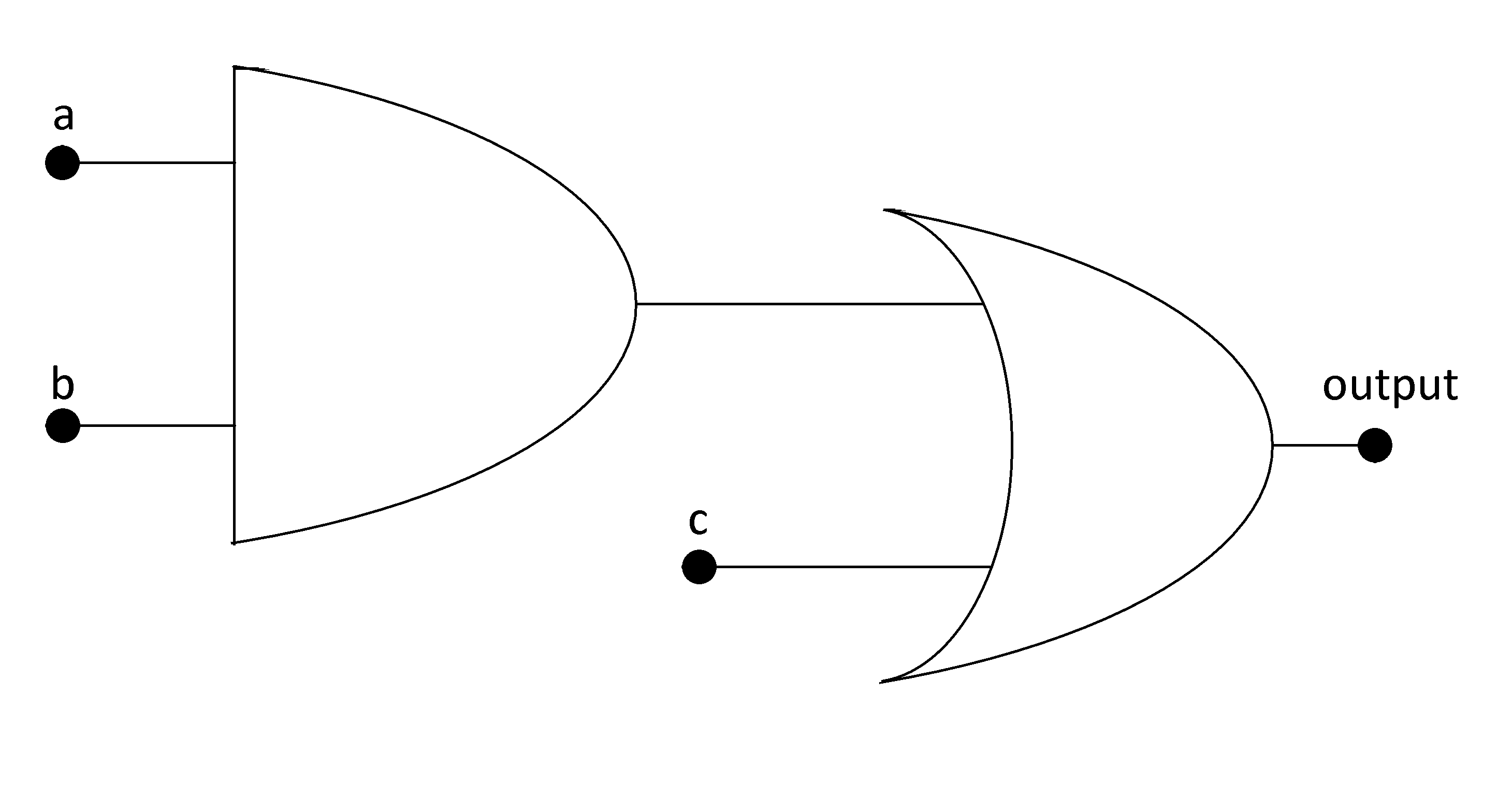
A Boolean function is a function that has n variables or inputs, so it has \(2^n\) possible combinations of the variables. These functions will assume only 0 or 1 in its output. An example of a Boolean function is this, f(a,b,c) = a X b + c. These functions are implemented with the logic gates.
Digital circuit of f(a,b,c)
a |
b |
c |
f(a,b,c) |
|---|---|---|---|
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
There is a way to implement functions in a canonical form, the minimal form of a function. For example if we had to implement a function with the truth table of the function f. First we would form the terms where the function has value 1, with only one possible combination of inputs for each term. The term would be 1 for one combination of inputs and 0 for all others. To do that we would use AND gates to make that combination of inputs equal 1 (note that if, for example, an input a is 0 we use !a in the gate). The function would then be a sum of all terms. So the terms of the truth table would be:
a |
b |
c |
f(a,b,c) |
Terms of the ∑ |
|---|---|---|---|---|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
!a X !b X c |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
!a X b X c |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
a X !b X c |
1 |
1 |
0 |
1 |
a X b X !c |
1 |
1 |
1 |
1 |
a X b X c |
With the laws of Boolean algebra a simplification to the implementation of the digital circuit with the minimal possible number of gates can be done; there is another way to implement the canonical function, which is to implement the negated function and then negate it again and use De Morgan laws to retrieve a product of terms. This is the dual form of the summatory. The function will now be a product of terms and the terms will have the value of 0 for one combination of the inputs and 1 for every other combination.
a |
b |
c |
!f(a,b,c) |
Terms |
f(a,b,c) |
Terms of the ∏ |
|---|---|---|---|---|---|---|
0 |
0 |
0 |
1 |
!a X !b X !c |
0 |
a + b + c |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
!a X b X !c |
0 |
a + !b + c |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
a X !b X !c |
0 |
!a + b + c |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
Operating the terms we get the basic form that is f = a X b + c.
De Morgan laws have another useful implication – we can use them to write a function as a combination of only NAND or NOR gates which use the least amount of transistors/space in the digital circuit.
In conclusion, there are two ways to retrieve the canonical form of a function; the sum of the terms or its dual, the product of the terms.